Ajustes de afinación
Logic Pro incluye un sistema de afinación en tiempo real para su uso con los instrumentos de software incluidos. Es posible configurar el sistema de afinación en los ajustes de proyecto de afinación.
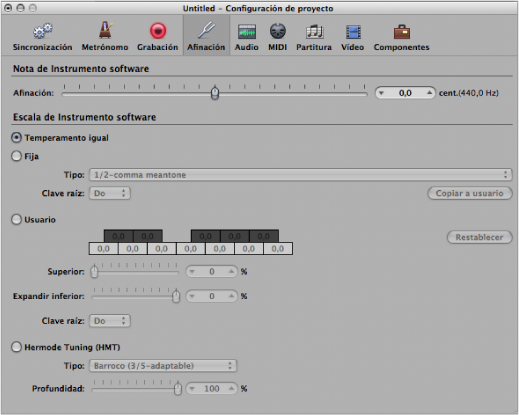
Seleccione Archivo > Ajustes del proyecto > Afinación (o use el comando de teclado “Abrir ajustes de afinación del proyecto”).
Haga clic en el botón Ajustes de la barra de herramientas Organizar y, a continuación, seleccione Afinación en el menú local.
- Botones de “Escala de Instrumento software”: seleccione el botón de adecuado de “Escala de Instrumento software” para activar escalas de afinación alternativas. La escala de afinación seleccionada se guarda con el proyecto y se vuelve a cargar la próxima vez que se abre el proyecto.
- Fija: activa una serie de escalas y teclas de afinación fija. El modo “Afinación fija” afina las notas en los sistemas de afinación escalada (según diferentes grados) y proporciona un carácter de armadura. Cuando se tocan principalmente teclas blancas (en el ajuste Puro y con Do como clave raíz), Do mayor es el centro principal y la afinación se escala a este acorde. Si se toca un acorde La mayor inmediatamente después de un Do mayor (y, por lo tanto, sujeto a la afinación escalada de Do mayor), el acorde La mayor se verá ligeramente afectado por el efecto de la afinación escalada, pero no sonará totalmente temperado. Si normalmente interpreta música polifónica, este modo (si usa el ajuste Puro) es el que mejor sonará. Las escalas de afinación fija son ideales para determinados instrumentos y estilos de música barrocos y medievales.
- Usuario: cuadros de Semitonos: desafine cada semitono por pasos, arrastrando verticalmente en cada caja de semitonos hasta el valor deseado. Alternativamente, puede hacer doble clic en cada caja de semitonos e introducir el valor deseado. Pulse Retorno o haga clic en otra caja para salir del modo de introducción de texto.
- Hermode Tuning: menú local Tipo: le permite definir diferentes modos de Hermode Tuning.
- “Clásico (3/5–todo)”: este modo proporciona una afinación amplia y regular de quintas y terceras puras. En casos de conflicto, el grado de pureza se reducirá temporalmente. Puede usar este modo para todo tipo de música. El valor del parámetro Profundidad indica el grado de pureza de las quintas y las terceras. Un valor de 100% determina la máxima pureza. El ajuste mínimo de pureza es el 10%. Desactivar ajusta la afinación a una escala de temperamento igual.
- “Pop/Jazz (3/5/7–todo)”: en este modo se cambian las quintas, terceras y séptimas. Es ideal para estilos de pop y jazz, especialmente si se usan acordes sostenidos. Sin embargo, no es muy apropiado para la música polifónica, ya que la desafinación de la séptima natural es bastante alta. Siempre debería utilizar este modo con un valor de Profundidad del 90% o el 100%, ya que otros valores harán que la séptima natural resulte acústicamente ineficaz.
- “Barroco (3/5–adaptable)”: este modo afina quintas y terceras puras (con características cambiantes). En música tonal, con un centro armónico claro, la afinación de los acordes centrales es muy pura, mientras que la de los acordes más distantes no lo es tanto. Si el centro armónico se vuelve borroso, todos los acordes serán afinados con la misma pureza. Igual que con el resto de los parámetros de modo, un valor de Profundidad del 100% determina la mayor pureza posible, y uno del 10% la menor.
Acerca de la afinación
En los apartados siguiente se proporciona información básica sobre la afinación.
Acerca de las afinaciones alternativas
La escala de 12 tonos que se usa actualmente en la música occidental ha tardado siglos en desarrollarse. Entre esas 12 notas se esconde una serie de microtonos (diferentes intervalos de frecuencia entre tonos).
Para explicarlo, examinemos la serie armónica: imagine que tiene una frecuencia de partida (o fundamental) de 100 Hz (100 vibraciones por segundo). El primer armónico es el doble de esa frecuencia, es decir, 200 Hz. El segundo armónico lo encontramos en 300 Hz, el tercero en 400 Hz, etc. Musicalmente hablando, sabemos que cuando se dobla la frecuencia, el tono se incrementa exactamente en una octava (en el sistema de 12 tonos). El segundo armónico (300 Hz) está exactamente una octava (y una quinta justa) por encima de la frecuencia fundamental (100 Hz).
A raíz de esto, podríamos deducir que lo lógico es afinar un instrumento a quintas puras. Al hacerlo, cabría esperar una escala perfectamente afinada desde el primer Do hasta el Do superior o inferior.
Para simplificar este ejemplo: imagine que está afinando un instrumento y empieza por una nota llamada Do con una frecuencia de 100 Hz. (Un Do real estaría más cerca de 130 Hz.) La primera quinta se afinaría ajustando el tono hasta obtener un tono totalmente claro, sin batidos (los batidos son modulaciones cíclicas del tono). El resultado sería un Sol a exactamente 150 Hz, que se deriva del cálculo siguiente:
La fundamental (100 Hz) x 3 (=300 Hz para el segundo armónico).
Dividido por 2 (para bajar hasta la misma octava que la nota inicial).
Esta relación se expresa frecuentemente en términos de una proporción 3:2.
Para el resto de la escala: afine la siguiente quinta hacia arriba: 150 x 3 = 450. Divida esta quinta por 2 para obtener 225 (que es más de una octava por encima de la nota de partida, por lo que tendrá que bajarla otra octava más, hasta 112,5).
En la tabla siguiente se resumen los diferentes cálculos.
Nota | Frecuencia (Hz) | Notas |
|---|---|---|
Do | 100 | x 1,5 dividida por 2. |
Do# | 106,7871 | Dividida por 2 para mantenerse en la octava. |
Re | 112,5 | Dividida por 2 para mantenerse en la octava. |
Re# | 120,1355 | Dividida por 2 para mantenerse en la octava. |
E | 126,5625 | Dividida por 2 para mantenerse en la octava. |
Fa (Mi#) | 135,1524 | |
Fa# | 142,3828 | Dividida por 2 para mantenerse en la octava. |
Sol | 150 | (x 1,5) dividida por 2. |
Sol# | 160,1807 | |
La | 168,75 | |
La# | 180,2032 | |
B | 189,8438 | |
Do | 202,7287 |
Tal como se puede ver en la tabla anterior, existe un problema.
A pesar de que las leyes de la física dictan que la octava superior a Do (100 Hz) es otro Do (a 200 Hz), el ejercicio práctico de un círculo perfecto (de Do a Do) de quintas exactas da como resultado un Do a 202,7287 Hz. No se trata de un error matemático. Si se tratase de un instrumento real, el resultado sería evidente.
Para evitar el problema, es necesario elegir entre las siguientes opciones:
Afinar las quintas perfectamente, a costa de octavas desafinadas, o
Afinar perfectamente las octavas, a costa de la quinta final (Fa a Do) desafinada.
El oído percibe con mayor facilidad las octavas desafinadas, por lo que la elección es obvia.
La coma
La diferencia entre una octava perfectamente afinada y la octava resultante de un círculo afinado de quintas se conoce como coma.
Durante siglos se ha optado por diferentes enfoques para resolver este misterio, obteniéndose varias escalas (llegando finalmente al concepto de temperamento igual: la escala de 12 tonos).
Otros temperamentos que se han ideado a lo largo de la historia maximizan o enfatizan diferentes aspectos de las características armónicas.. Todos ellos llegan de un modo u otro a un compromiso. Algunos maximizan las terceras puras (tono medio) y otros enfatizan las quintas puras a costa de las terceras (Kirnberger III, por ejemplo).
Cada temperamento tiene su propio carácter, por lo que una pieza de música puede sonar bien en un tono y horrible en otro. La transposición de una pieza a otro tono puede cambiar por completo su carácter.
Debe prestar mucha atención a la selección de temperamentos si desea realizar interpretaciones auténticas de música histórica para teclado. Una elección equivocada puede conllevar una experiencia musical insatisfactoria e históricamente inexacta.
Acerca del temperamento igual
El temperamento igual toma el error (la coma) y lo reparte equitativamente entre todos los pasos de una escala cromática. Como resultado, se obtiene una escala de intervalos idénticamente mal afinados, con ninguno de ellos claramente desafinado pero ninguno perfectamente afinado. El temperamento igual se ha convertido en un estándar de facto por dos motivos:
- Comodidad: volver a afinar un instrumento según un temperamento determinado más apropiado para una pieza de música particular es un fastidio. Muchos instrumentos no se pueden afinar de manera alternativa (instrumentos de cuerda con trastes, por ejemplo).
- Movilidad: todas las piezas musicales occidentales pueden ser interpretadas (adecuadamente) en un instrumento afinado según el temperamento igual. Obviamente, puede que se pierdan algunos matices de las piezas que originalmente se interpretaban con otro temperamento.
¿Qué es Hermode Tuning?
Hermode Tuning controla automáticamente la afinación de los instrumentos de teclado electrónicos (o los instrumentos de software de Logic Pro) durante las interpretaciones musicales.
Para poder crear frecuencias claras para todos los intervalos de quintas y terceras en todas las progresiones posibles de acordes e intervalos, un instrumento de teclado necesitaría muchas más teclas por octava de las 12 que tiene.
Hermode Tuning puede ayudarle con este problema: mantiene la relación de afinación entre teclas y notas, a la vez que corrige las notas individuales de los instrumentos electrónicos, asegurando de este modo un alto grado de pureza. Este proceso consigue por nota hasta 50 frecuencias escalonadas con precisión, a la vez que mantiene la compatibilidad con el sistema de afinación fija de 12 notas por octava.
Funcionamiento de Hermode Tuning
La corrección de frecuencias se basa en las estructuras de los acordes analizadas.
Se analiza la posición de las notas individuales de cada acorde, y la suma de las distancias de cada nota a la escala temperada es puesta a cero. En casos críticos, diferentes funciones de compensación ayudan a mantener bajo el nivel de reafinación, aunque sea a costa de la pureza absoluta.
Ejemplos:
Las notas Do, Mi y Sol forman un acorde de Do mayor.
Para afinarlas armónicamente, la tercera (el Mi) tiene que estar afinada 14 centésimas (de semitono temperado) por encima, y la quinta (el Sol), 2 centésimas por encima.
Recuerde que Hermode Tuning no es estática, sino dinámica. Se ajusta continuamente al contenido de la música. Esto es así porque, como alternativa a la afinación normal o temperada, los intervalos de quinta y tercera también se pueden afinar según algunas proporciones de frecuencia ideales: la quinta con una proporción de 3:2 y la tercera mayor, de 5:4. Las tríadas mayores sonarán muy sólidas.
Con una afinación limpia (escalada), Hermode Tuning cambia las frecuencias a valores parcialmente superiores o inferiores.