Sound Basics
Prior to considering any of the sound-generating components you will find in a synthesizer, it’s important that you understand sound itself.
Technically, sound is the conversion of physical energy—such as a hand clap—to an air pressure disturbance. This change in air pressure is transmitted as a series of vibrations—a sound wave—through the air. Sound vibrations can also be transmitted through other matter, such as a wall or floor.
If the vibrations follow a periodic pattern, the sound is said to have a waveform.
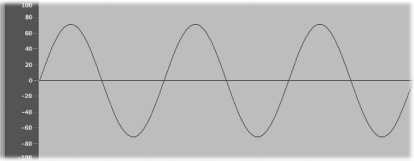
The figure above shows an oscillogram—a graphical representation—of a sine wave, the simplest and purest kind of waveform.
If the vibrations do not follow a discernible pattern, the sound is called noise.
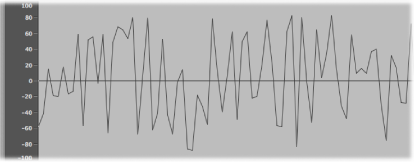
A repetition of a waveform—each peak and trough in the oscillogram—is known as a cycle. The number of cycles that occur per second determines the basic pitch of the waveform—commonly known as the frequency. Most Logic Pro instruments provide a Hz (Hertz) or Frequency control that determines the number of cycles per second—and therefore the pitch.
Tones, Overtones, Harmonics, and Partials
The frequency of a sound is known as its fundamental tone.
The waveforms of all sounds, apart from a basic sine wave, consist of the fundamental tone and many other tones of different frequencies. Nonfundamental tones that are whole-number multiples of the fundamental tone are known as overtones or harmonics. Nonfundamental tones that are multiplied by fractional amounts (not whole numbers) are called partials. A tone divided by the frequency of the fundamental tone is referred to as a subharmonic.
The fundamental tone is referred to as the first harmonic. This is generally louder than the other harmonics.
A tone played at twice the frequency of the first harmonic is called the second harmonic.
A tone played at four times the frequency of the first harmonic is called the fourth harmonic, and so on.
Each of these harmonics has a different timbral quality from the fundamental tone. In general, harmonics that can be multiplied or divided by a whole number–such as octaves, odd-numbered or even-numbered harmonics, and so on–sound more “musical.”
Tones that cannot be multiplied or divided by a whole number are known as inharmonic overtones, or partial tones. When you combine a number of these inharmonic overtones, it tends to sound “noisy.”
The Frequency Spectrum
A fundamental tone, when combined with various harmonics of different levels, is perceived as a sound. The level relationships between these sonic elements change over time (controlled by envelopes, discussed later in this appendix). The combination of a number of harmonics is referred to as the harmonic spectrum or, more commonly, the frequency spectrum.
The frequency spectrum shows all the individual sonic elements in a sound. It is shown low to high from left to right. The respective levels of all harmonics are reflected vertically, with taller spikes indicating higher levels.
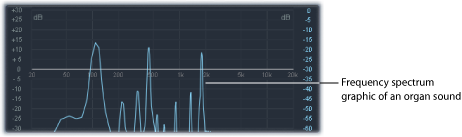
The illustration shows the level and frequency relationships between the fundamental tone and the harmonics at a particular moment in time. These relationships constantly change over time, which results in continuous changes to the frequency spectrum and, therefore, changes to the sound.
Other Waveform Properties
A sound wave, as discussed earlier, has a frequency. Other properties of sound waves include amplitude, wavelength, period, and phase.
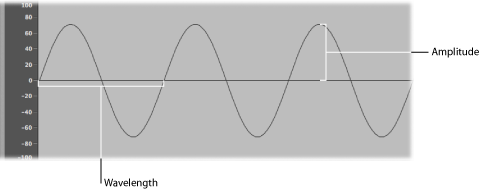
- Amplitude: The amplitude of a waveform indicates the amount of air pressure change. It can be measured as the maximum vertical distance from zero air pressure, or “silence” (shown as a horizontal line at 0 dB in the illustration). Put another way, amplitude is the distance between the horizontal axis and the top of the waveform peak, or the bottom of the waveform trough.
- Wavelength: The wavelength is the distance between repeating cycles of a waveform of a given frequency. The higher the frequency, the shorter the wavelength.
- Period: The (wave) period is the amount of time it takes to complete one full revolution of a waveform cycle. The higher and faster the frequency, the shorter the wave period.
- Phase: Phase compares the timing between waveforms and is measured in degrees—from 0 to 360.
When two waveforms begin at the same time, they are said to be in phase or phase aligned. When a waveform is slightly delayed in comparison to another waveform, the waveforms are said to be out of phase.
Note: It is difficult to discern a constant phase difference over the entire wave period, but if the phase of one of the waveforms changes over time, it will become audible. This is what happens in common audio effects such as flanging and phase shifting.
When you play two otherwise identical sounds out of phase, some frequency components—harmonics—can cancel each other out, thereby producing silence in those areas. This is known as phase cancellation, and it occurs where the same frequencies intersect at the same level.
