音の基礎
シンセサイザーに内蔵されているサウンド生成コンポーネントについて考慮する前に、サウンド自体について理解しておくことは大切です。
技術的な観点から述べると、音は物理エネルギーの変換です。たとえば、手を叩くことで、空気圧が乱されます。この空気圧の変化が、一連の振動(音波)として空気中を伝わります。音の振動は、壁や床などのほかの物体にも伝えることができます。
振動に一定のパターンがある場合、その音には波形があると言います。
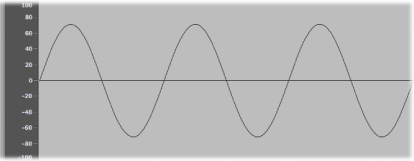
上の図は、最もシンプルで純粋な波形である正弦波のオシロスコープ波形を示します。
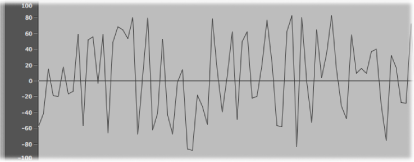
振動に識別可能なパターンがない場合、その音はノイズと呼ばれます。
波形の反復(オシロスコープ波形のそれぞれの山と谷)はサイクルと呼ばれます。1 秒間に発生するサイクル数により、周波数と呼ばれる波形の基本ピッチが決まります。「Logic Pro」の大半の音源には、1 秒あたりのサイクル数(ピッチ)を調整する Hz(ヘルツ)または周波数のコントロールが備わっています。
トーン、倍音、ハーモニック、および部分音
サウンドの周波数は、その基音で識別されます。
すべてのサウンドの波形は、基本的な正弦波を除き、基音および周波数の異なる多数のトーンで構成されます。基音を整数倍した基音以外のトーンは、倍音またはハーモニックと呼ばれます。基音に(整数ではなく)小数をかけた基音以外のトーンは、部分音と呼ばれます。基音の周波数で除算されたトーンは、サブハーモニックと呼ばれます。
基音は、1 次ハーモニックとも呼ばれます。これは通常、ほかのハーモニックよりも音量が大きくなります。
1 次ハーモニックの 2 倍の周波数で演奏したトーンは、2 次ハーモニックと呼ばれます。
1 次ハーモニックの 4 倍の周波数で演奏したトーンは、4 次ハーモニックと呼ばれます。ほかのハーモニックも同じ方法で命名されます。
これらの各ハーモニックは、音質が基音とは異なります。一般に、整数(オクターブ、奇数または偶数のハーモニックなど)で乗算または除算可能なハーモニックは、より音楽性の高いサウンドになります。
整数で乗算または除算できないトーンは、不協和倍音または部分音と呼ばれます。これらの不協和倍音をいくつも組み合わせると、「ノイズの多い」サウンドになります。
周波数スペクトル
基音をレベルの異なるさまざまなハーモニックと組み合わせると、サウンドとして聞こえます。これらの音響要素間の相対的なレベルは、時間の経過と共に変化します。変化の制御にはエンベロープを使用します。エンベロープについては、この付録の後の部分で説明します。多数のハーモニックを組み合わせたものをハーモニックスペクトルまたは周波数スペクトルと呼びます。後者の名称の方が一般的です。
周波数スペクトルには、サウンド内の個別の音響要素すべてが表示されます。これは、下から上に、および左から右に表示されます。ハーモニックの各レベルは、上下方向に反映されます。スパイクが高いほど、音量が大きいことを表します。
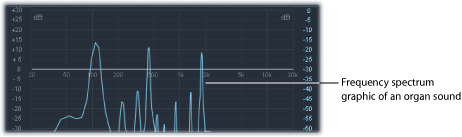
図は、ある時点の基音とハーモニック間に見られる音量と周波数の関係を表しています。これらの関係は時間と共に絶えず変化するため、周波数スペクトルが継続的に変わってゆきます。その結果、サウンドが変化します。
そのほかの波形プロパティ
すでに説明したように、音波には周波数があります。音波のほかのプロパティには、振幅、波長、周期、および位相などがあります。
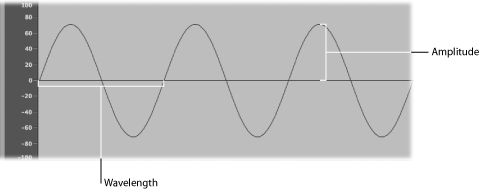
- 振幅: 波形の振幅は、音圧の変化を示します。これは、音圧ゼロまたは無音(図では 0 dB の水平線)からの最大垂直距離で表します。言い換えると、振幅は、水平軸から波形の山の上端または波形の谷の下端までの距離です。
- 波長: 波長は、特定の周波数の各波形サイクル間の距離です。周波数が高くなるほど、波長は短くなります。
- 周期: (音波の)周期は、1 つの波形サイクル全体にかかる時間を指します。周波数が高く、早くなるほど、周期は短くなります。
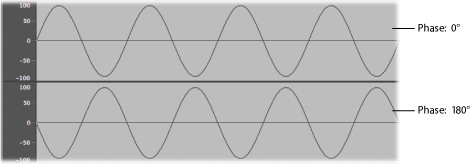
- 位相: 位相は波形間のタイミングを比較するもので、0° 〜 360 ° までの度数で表します。
2 つの波形が同時に始まる場合、それらは同相であるまたは位相が揃っていると言います。ある波形が別の波形よりも若干遅れている場合、これらの波形は位相を外れていると言います。
メモ: 周期全体にわたる固有の位相差を聞き分けるのは難しいことですが、いずれかの波形の位相が時間の経過に伴って変化する場合には、変化を聞き取ることができます。これは、フランジングや位相シフトなどのオーディオエフェクトでよく発生します。
位相はずれているが、それ以外では同一の 2 つのサウンドを演奏する場合、一部の周波数成分(倍音)が互いに打ち消し合い、その部分が無音になることがあります。これは位相の打ち消しと呼ばれ、同じ周波数が同音量で交差する場合に発生します。